An Isochronous Curve makes an Aestetically Pleasing Bowl

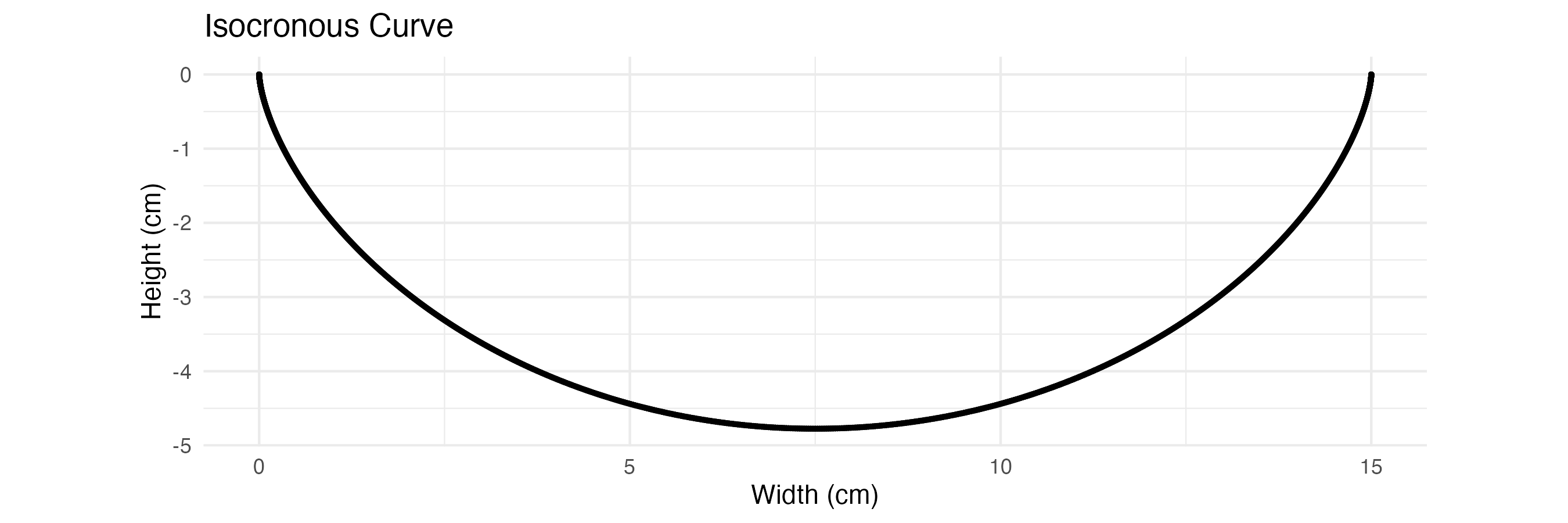
An isocrous curve is a type of cycliod with many unique properties. Considering no friction and equal gravity, objects released anywhere on the curve will reach the bottom at the same time. The curve happens to be the trace of a fixed point on a circle as the circle rolls a whole rotaion. that is to say, as a circle with radius \(r\) rolls along the \(x\) axis,

\[x = r \,(t - \sin t)\] \[y = r \,(1 - \cos t)\]

for \(0 < t < 2\pi\)

A bowl with this curvature has the implicaiton that any two frictionless cheerios released anywhere on the bowl will colide in the middle at the same time. Also, the lip of the bowl is perfectly verticle, making it useful for chasing anything up the wall of the bowl with your spoon or chip.

To build the parametric deisgn, I used a nested for loop to plot 10,000 points and then drew a surface between:

Diameter=15 # the diameter of the bowl
a=Diameter/(2*pi) #the radius of the circle with this circumfrance 

bowl_df <- data.frame(x = numeric(0), y = numeric(0), z= numeric(0)) #initialising my data frame 
for (i in 0:99) {
  theta<-pi*(1/99)*i #100 points between 0 and pi 
  r=a*((pi-sin(pi))-(theta-sin(theta)))#100 radii, starting at apex of cycliod.
  for (k in 0:99) { # converting from cylindrical to cartesian coordinates: 100 points
    x<- r*cos(2*pi*.01*k) #x cordinate
    y<-r*sin(2*pi*.01*k) #y cordinate
    z<-2*a-a*(1-cos(theta)) #z cordinate is flipped so the bowl is upright (starts at 2p)
    bowl_df <- rbind(bowl_df, data.frame(t=t,h=h, x = x, y = y, z=z))
    }
}

The resulting 3-d rendering has a plesant shape, based on a simple yet elegant curvature. 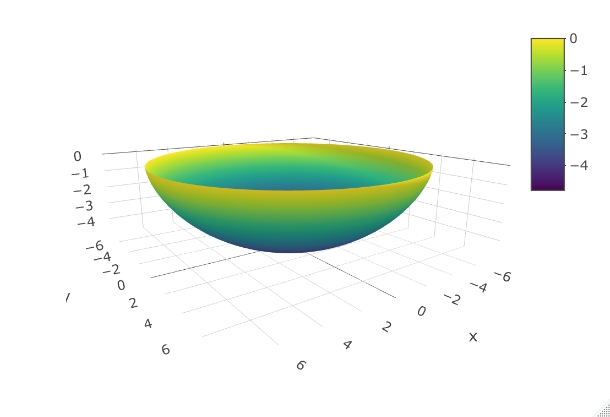Please let me know what you think. I am considering manufacturing a couple cermaic bowls.